Ôn, luyện thi đại học môn toán 2013 chú ý phương trình, hệ phương trình
Mặc dù cấu trúc đề thi đại học môn toán năm 2013 vẫn chưa được bộ GD-ĐT công bố nhưng nhìn chung không có nhiều thay đổi so với cấu trúc đề thi đại học môn toán các khối A, A1, B, D các năm trước, đặc biệt là năm 2012. Các bạn đang luyện thi đại học nên đặc biệt chú ý phương trình lượng giác, phương trình vô tỉ, hệ phương trình...
Bài liên quan:
- Cấu trúc đề thi Đại học môn Toán năm 2013
- Các dạng bài tập toán về số phức để tham khảo
- Luyện thi đại học môn Toán: các công thức cần nhớ về hàm số và đồ thị
- Luyện thi đại học môn Toán: kiến thức cơ bản về Lượng giác
- Kỹ năng ôn thi đại học môn Toán
- Bí quyết luyện thi đại học khối A của thủ khoa đạt điểm tuyệt đối 31/30
- Kinh nghiệm luyện thi đại học khối D của một thủ khoa: học đâu chắc đó
- Để làm bài thi trắc nghiệm đại học 2013 hiệu quả
Khảo sát sự biến thiên của hàm số và vẽ đồ thị
Cần ghi nhớ cấu trúc lời giải của 3 dạng hàm số sau
Lưu ý khi vẽ đồ thị:
- Không được vẽ đồ thị ra ngoài mặt phẳng tọa độ.
- Nét vẽ đồ thị phải trơn, không có chỗ gấp khúc. Thể hiện sự "uốn" của đồ thị tại các điểm uốn.
- Đánh dấu tọa độ của các giao điểm của đồ thị với 2 trục tọa độ; các điểm cực đại, cực tiểu; điểm uốn (nếu có).
Phương trình lượng giác
Ghi nhớ các công thức lượng giác, quan hệ giữa các góc lượng giác, giá trị lượng giác của các góc đặc biệt và cách giải các dạng phương trình lượng giác được nêu trong SGK.
Thông thường ta nên hạ bậc các biểu thức lượng giác bậc cao về các biểu thức lượng giác bậc thấp hơn có trong phương trình để dễ dàng đưa về phương trình tích.
Nếu trong phương trình chủ yếu là các hàm lượng giác sin và cos thì ta nên biến đổi các hàm tan và cot về các hàm sin và cos.
Phương trình (vô tỉ), bất phương trình (vô tỉ), hệ phương trình, phương trình logarit
Thuộc các công thức logarit.
Nắm rõ cách giải các pt, bpt cơ bản.
Ứng dụng thành thạo 2 phương pháp giải hệ phương trình cơ bản là PP thế và PP cộng đại số, trong đó PP thế là PP được ứng dụng nhiều nhất.
Nắm rõ cách giải các dạng hpt thông dụng: đối xứng loại 1, loại 2; hệ đẳng cấp.
Nhiều phương trình, bất phương trình và hệ phương trình có thể giải dễ dàng bằng cách đặt ẩn phụ (thông thường ta phải biến đổi một chút để có thể nhìn ra ẩn phụ cần phải đặt).
Nguyên hàm, tích phân
Nắm rõ nguyên hàm của các hàm thông dụng.
Nắm rõ 2 phương pháp thông dụng để tính tích phân: phương pháp đổi biến và phương pháp tích phân từng phần:
- Phương pháp đổi biến thường áp dụng cho các hàm đa thức, phân thức và có chứa căn thức.
- Phương pháp tích phân từng phần thường áp dụng cho những hàm có dạng tích của 2 biểu thức khác nhau về bản chất: đa thức – lượng giác, đa thức-hàm mũ, đa thức – hàm logarit, lượng giác- hàm mũ.
Lưu ý về tích phân của hàm số lẻ, hàm số chẵn.
Trong một số trường hợp, ta có thể đổi biến bằng cách đặt.
Hình học không gian
Nắm vững công thức tính thể tích của các khối thông dụng.
Ứng dụng các định lí về quan hệ vuông góc, quan hệ song song trong không gian để tạo được mối liên hệ giữa độ dài các cạnh và các góc, qua đó tính được độ dài các cạnh và số đo của các góc chưa biết.
Bất đẳng thức, cực trị
Nắm vững các bất đẳng thức thông dụng, đặc biệt là BĐT Cô-si và BĐT Bu-nhi-a-cốp-xki.
Với một số bài toán tìm cực trị của hàm nhiều biến, ta nên quy về cực trị của hàm 1 biến rồi dùng ứng dụng của đạo hàm trong việc tìm min, max của hàm số.
Phương pháp tọa độ trong mặt phẳng và trong không gian
Nên ghi định hướng làm bài (sơ đồ giải) trước khi giải.
Số phức
Một số bài toán có thể ứng dụng công thức Moa-vrơ nếu có thể đưa các số phức về dạng lượng giác của các góc đặc biệt.


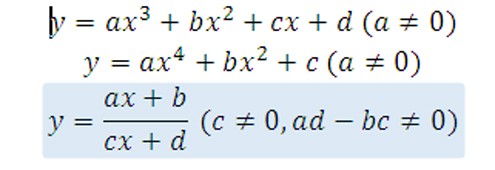
Thảo luận: